Content warning: If you are a mathematician the words I use below are bound to be formally inaccurate, sorry!
Origins:
I saw this post by Sofinho, which I thought was interesting (you should check it out). To cut a long story short, it led me here:
A D66 table with a probability gradient:
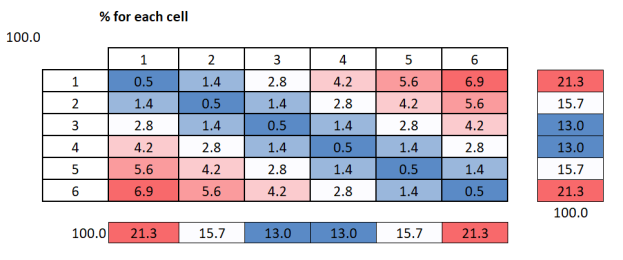
So the chance of rolling 1,1 is 0.5% and the chance of rolling 1,6 is 6.9%.
D6(6)6 Rules
- Roll 3D6
- Keep the highest & lowest rolls to make a D66 style dice
- Order these two dice how you like; or if that bothers you (perhaps you worry about an unconscious bias), order the two dice low to high if the removed middle roll is odd, else the other way round
Examples
- 6,5,1 becomes –> 1, 6
- 2,5,2 becomes –> 5,2
- 4,2,3 becomes –> 2,4
Below is the same table as above, but normalized so the lowest value is 1:
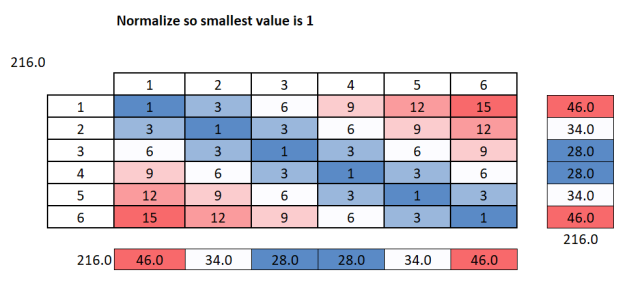
So rolling a 1,6 is 15 times more likely than rolling a 1,1.
Below is basically the same as above but where each cell is given with reference to % above/below a (standard homogeneous) D66 table, which is about 2.8% per cell:
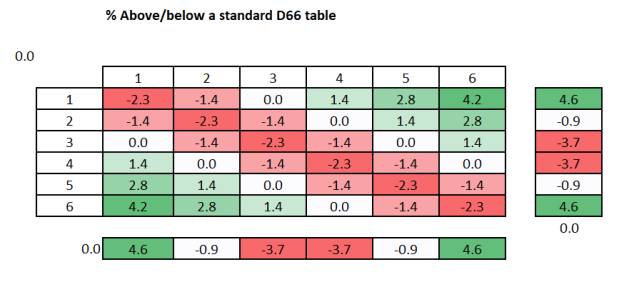
So cell 1,1 is 2.3% lower in probability than if this was a standard D66 cell.
Conclusions
- The diagonal ‘spine’ is disfavoured
- The top right and bottom left directions are more favoured (so, a 1,6 or 6,1 roll is 15 times more likely than any double)
- For probability, moving up/down gives the same result as moving right/left (so moving downward from 1,1 to 1,6 is the same as moving left to right from 1,1 to 6,1.
- Moving diagonally does not change the % odds, so rolling a 1,1 is the same % as rolling a 2,2 or 3,3 etc.
With this probability structure understood, you can create D66 random tables that are less homogeneous.
– – –
>> This is where you should stop reading, as I go (more) tangential below <<
- For now if you ignore half the table (in this case ignoring the results above the diagonal spine) there appears to be a series of tiers (e.g. 1,1 to 1,6; 2,2 to 2,6; 3,3 to 3,6 etc.):
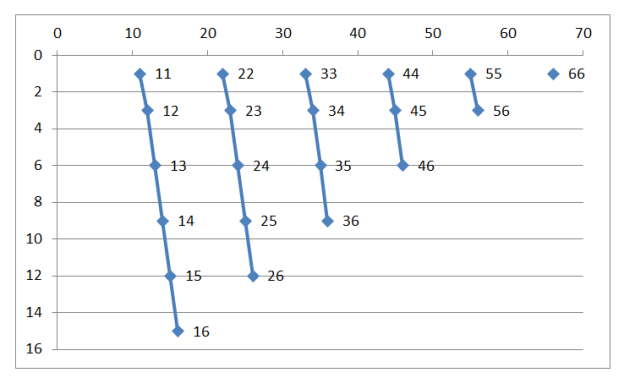
These tiers are not equal in size, each starts with a low % and increases as you move along the tier away from the diagonal spine. So the tier 1,1 to 1,6 is bigger than the tier 3,3 to 3,6 – I suppose there are also diagonal tiers, again not of equal size but in that case each step in the tier has the same %.
These sort of tiers made we wonder – can we use this method to make a series of tiered random tables?
City encounter/reaction tables
Examples are always best, so I’m going to consider a way this method could be used to generate random reaction encounters in a D&D type city.
In this case, I’m going to link the tiers to social class in the city, using this colour code:
So the above tiers would be:

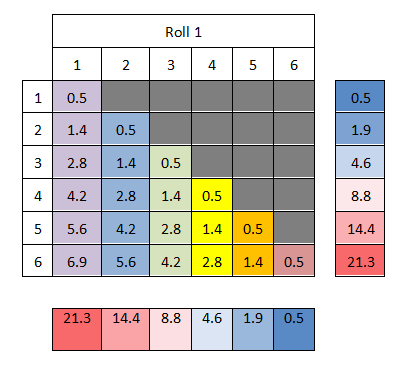
 Again, for now I’m only considering the lower half of the table (so not the greyed out area).
Again, for now I’m only considering the lower half of the table (so not the greyed out area).
In this case the beggars/riffraff/lowest class tier interact most often with the PCs (21.3% of the time, i.e. whenever the first roll is a 1), whereas nobles rarely interact with the PCs i.e. only on a roll of 6,6 (0.5% of the time).
As for reactions, the nobles only have 1 reaction state, which in this case is probably indifference (at best).
However, the beggars/riffraff tier have 6 reactions states i.e. 1,1 (0.5% of the 21.3%) to 1,6 (6.9% of the 21.3%). So while there are 6 reaction states, 1,6 is the most probable reaction and so this should be the most common reaction state (e.g. asking for money) and 1,1, should be quite unusual (e.g. giving the PCs a gift or perhaps attacking them).
So perhaps the above structure makes sense in a dodgy market bazaar area (or slums), where beggars/riffraff are going to be out and about, and where other people including nobles might be out looking for something unusual/special (but on their guard, i.e. with 1 reaction state).
If you inverted the social structure (so the nobles have the 6 reaction states and are common), perhaps this makes sense in an upmarket retail area (or in the royal court) , where beggars/riffraff are going to be circumspect. Perhaps in the royal court the single riffraff state is a person intent on the redistribution of wealth.
Now if we bring in the rest of the table we blanked off earlier, you get the same tiers but in this case they also move left to right not just up/down. Perhaps the portion above the diagonal spine could be negative reaction states and below the diagonal spine could be positive reactions states e.g.:
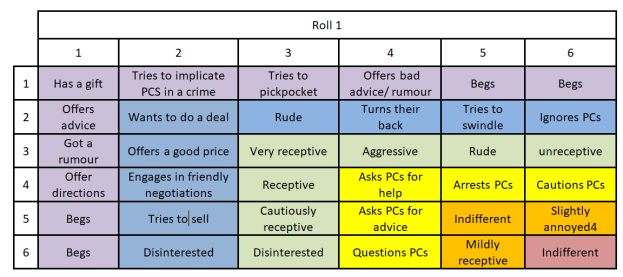

42% 28.2% 17% 8.8% 3.2% 0.5%
OK, looking at this – that’s a lot of beggars/riffraff approaching the PCS in this city area, so perhaps swap town’s person for either beggars or for the merchants … ? That said, perhaps town’s folk are the decent kind of folk that stays well away from disreputable freebooters like the PCs.
Another option is to keep the greyed off area as a “no significant encounter” option.
Other uses …
The above is the first idea that sprang to mind. There must be other uses – tiers/kinds of random wilderness encounters, etc … or (probably for the best) just ignore tiers and populate the D6(6)6 table in a manner that takes account of where there probabilities are high/low.
I’m still not the RPG police …
If you don’t like this idea (and I’m just thinking this through) you don’t have to use it …
– – –
Me on DriveThru; at the moment I’m mainly pimping my procedural:
:: High Seas ‘Hex Crawl’ – In the Heart of the Sea,
:: Wilderness Hex Crawl – In the Heart of the Unknown,
:: Dungeon/network generator – In the Heart of the Delve & Dangerous
