I’ve not been blogging much lately as I’ve been following the invasion of Ukraine by the genocidal regime in Russia. You can donate to a reputable aid charity to help Ukraine here (LINK).
So, to break out of the rut, I thought I’d post something RPG-ish (see the title above – edited to add the ‘Markov dice?’ tag)
Edit – Of course, other systems could be used instead of this idea (sure, there are always other ways of doing things). One benefit of this idea is that you do not need a separate supporting reference piece of paper, the idea is that the dice should be self-policing and anyway people enjoy rolling those math rocks
:O)
Background
I’ve posted quite a lot about Hex Flowers ‘Random Tables with a inbuilt memory‘.
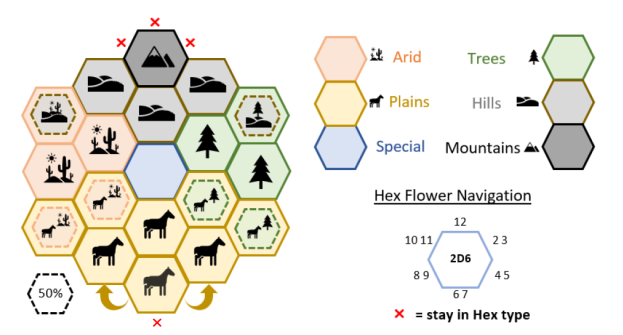
The above is from In the Heart of the Unknown Hex Flower
The idea is that the last roll affects the result you are about to make – hence the ‘inbuilt memory’ effect. People often tell me that these are Markov Chains bound in a hexagon of hexagons framework (with some rules and stuff).
The dice memory thing you mentioned?
I recently (well last night) wondered if you could do a similar thing with a set of dice.
The idea being you a roll a die with set solutions, which then takes you to a new die, again with new set solutions. So, like a hex flower, but where you change dice, not the location on a Hex Flower. This has probably been suggested by someone before …
Let’s do an example …
Let’s do this with a set of D12s:
You can draw a D12 like this (this flattened out drawing probably has a fancy name):
Plains die:
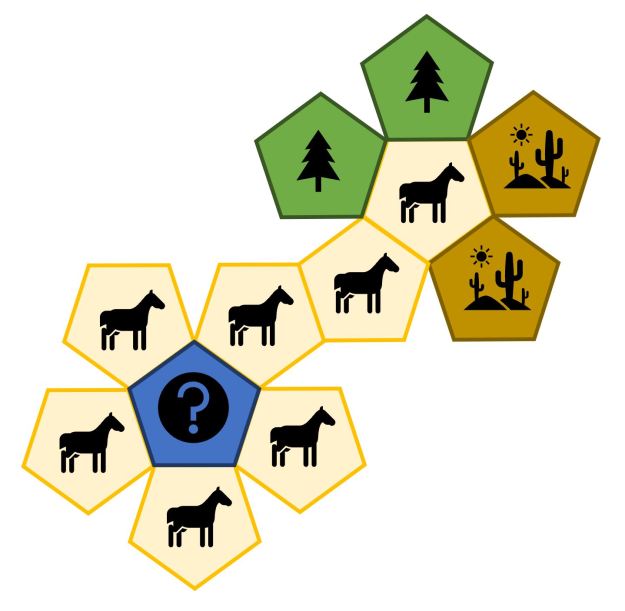
When on plains roll this die to see what terrain comes next. The most likely result is more plains, but there is a smaller chance to get an ‘arid’ or ‘trees’ hex, or even a ‘special’ terrain hex ‘?’.
If you roll the above D12 and get: (a) plains the next hex is plains; but if you roll: (b) the next hex is an ‘arid’ hex etc.
Next turn find the die that corresponds to the present hex i.e. the one you just moved to (e.g. in the above example: (a) = roll the plains die again; and in case of (b) = roll the arid die) and roll that die to find out what the next hex is.
Rinse and repeat.
Arid die:
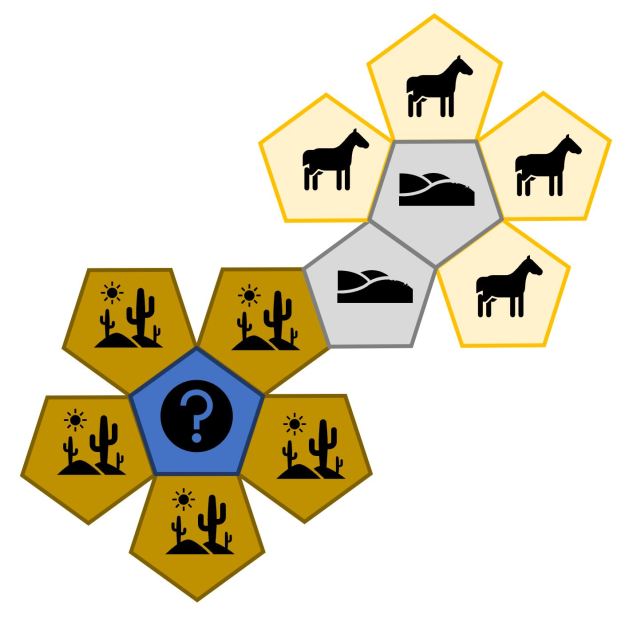
The arid D12 mainly returns more arid hexes, but the next hex could be plains or even hills (again there is a chance for a ‘special’ hex.
Trees die:
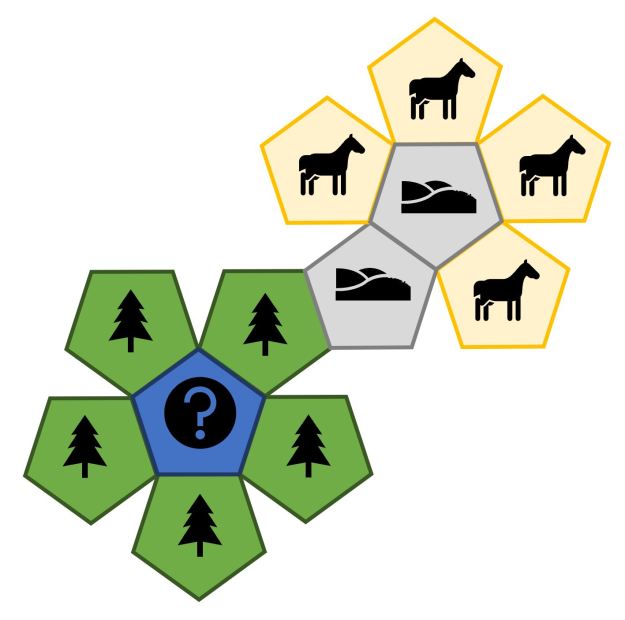
Like above, but mainly trees are returned with this D12.
Hills die:
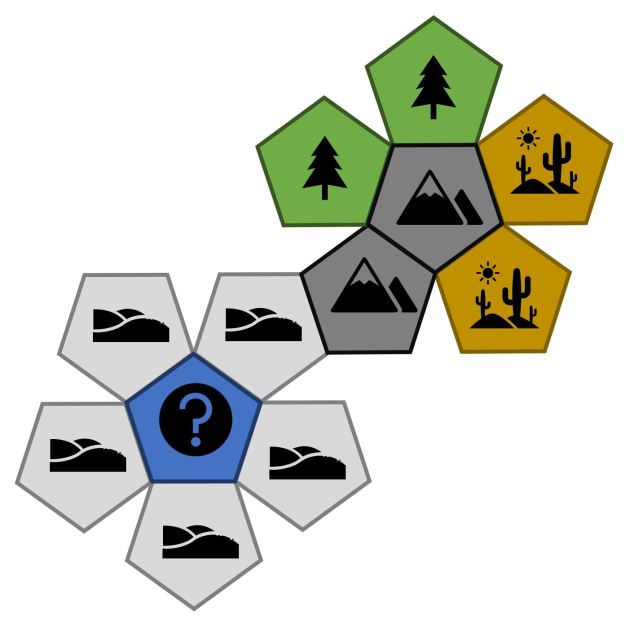
Like above, but there is now a chance for Mountain hexes (note, there is no way to get to mountains without going via the Hills die (… well not unless you go via the ‘special die’, but that is why it is there, a bit of a wild card option, but is very much the exception).
Mountains die:
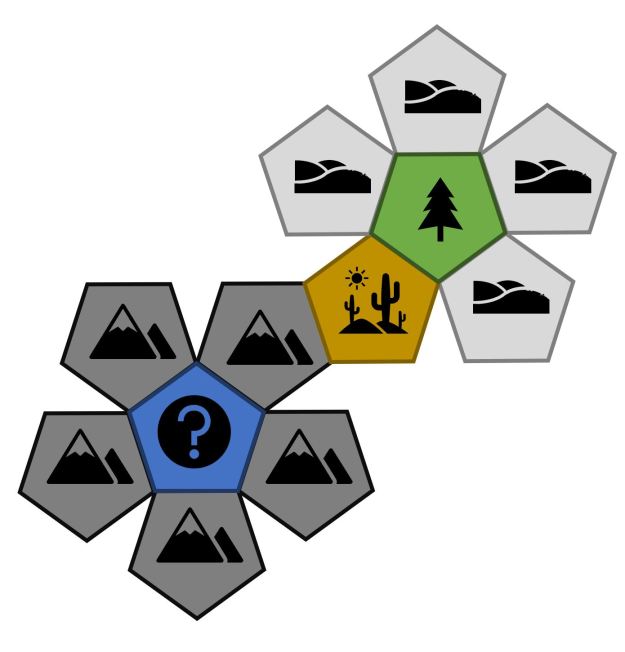
Again, mountains tend to return more mountains – e.g. like a mountain range. I’m torn between replacing ‘arid’ and ‘trees’ with more ‘mountains’ and let the ‘wild card’ take care of any trees / arid hexes. This would increase the change of getting a mountain range (which I like the idea of).
Special (confirmation die):
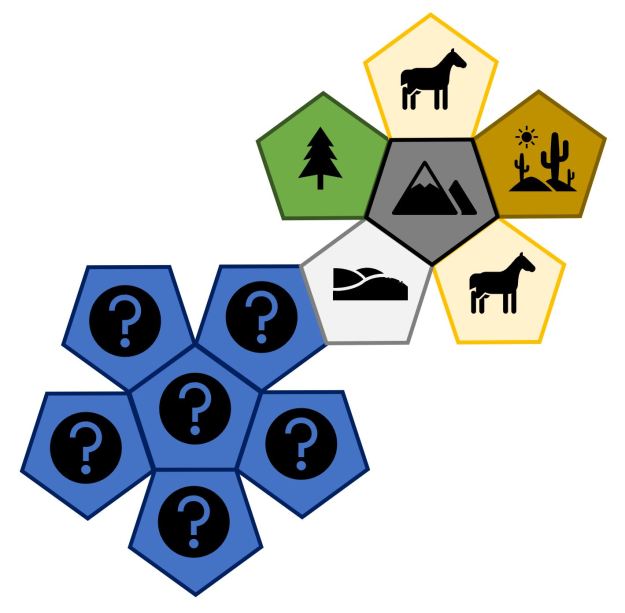
I’d use the ‘Special die’ to confirm if the next hex feature is really ‘special’ e.g. lake, meteor crater, waterfall etc., or if it is just one of the other terrain types, which might still be an unusual ‘special’ transition e.g. mountains to plains.
You could make a set of these dice for weather, or basically anything. Like Hex Flowers you could build any minigame e.g. mass combat dice set to model the ebb and flow of a battle etc.
Other dice e.g. D20?
The above is just an example (just brain storming) and not optimised. D20s would give more options, but the faces are quite small. D12 seems like a good compromise on face size and number of options.
Well that’s it, I just need a Kickstarter to make the dice!
The Pink Phantom trying it out (with his water modification)
I like this water symbol idea from TPF.
My instincts might be to keep going with water until you roll another blue symbol. So the blue symbols toggle the water on/off. Maybe having one blue symbol per D12. Of course, players could choose not to follow the water course, e.g. crossing over the river. In which case, the water would end (for now). Might need something for roads …
In my ItHoTU, I had a separate HF for roads, rivers, encounters and settlements etc. I’d need to think about how to do this using this dice setup.
What is a Hex Flower anyway?
It is a bit like a random table, but with an inbuilt memory. To find out more check out my Hex Flower Cookbook which is now platinum best seller on DriveThruRPG and PWYW.
Were-reindeer cult
Of course, the idea is for people to use the code if they cannot afford to buy a copy (life stuff). There is no date limit on this offer, but after 10 uses the code will expire.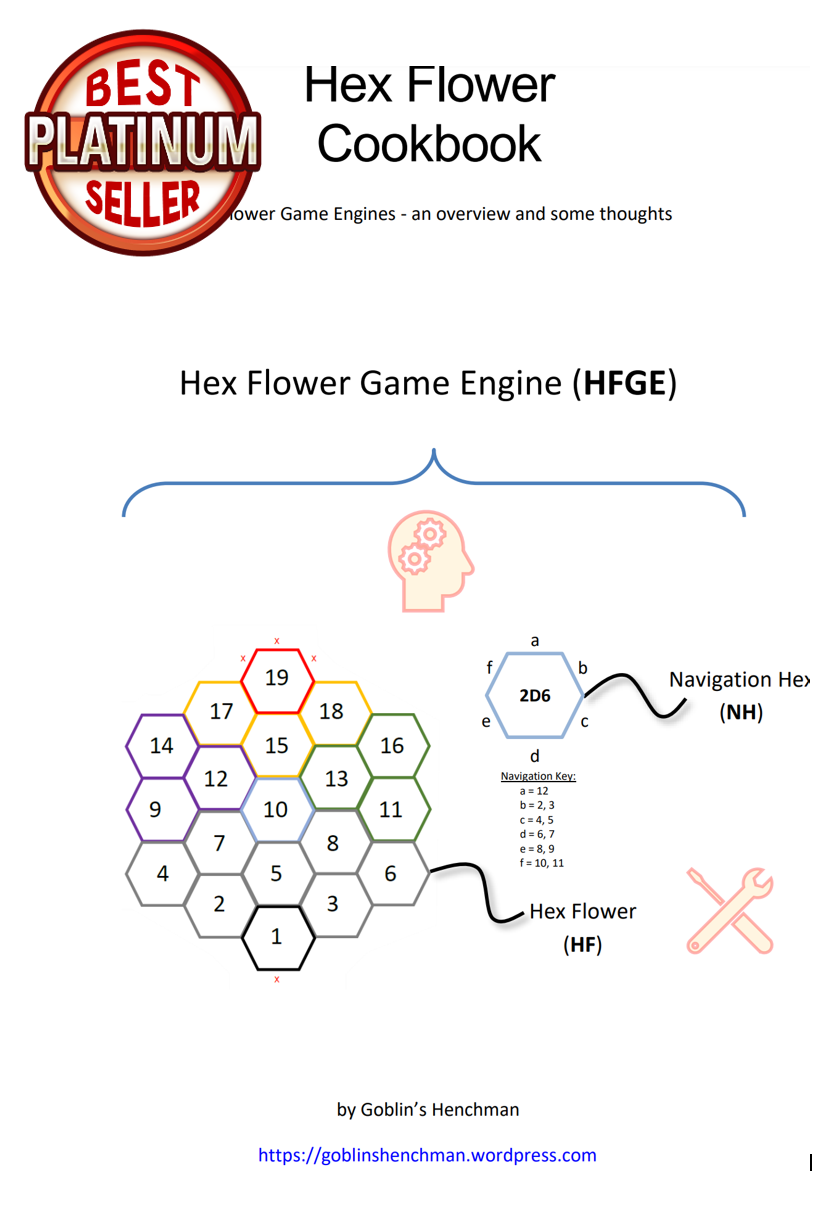
Pass & Pass – player knows and I’d say the PC also knows they passed the test, because they know they did a good job (the uncertainty/opacity die is almost a self-evaluation roll – in real life we have all done a examination/test etc. that we know we have failed and vice versa. Knowing you failed can be useful even if it is not the desired result).
Pass & Fail – this is where it gets more interesting, the player and PC do not know if they passed the test – they are getting mixed information:
Fail & Fail – The player and the PC know that they bungled the attempt and so cannot make any meaningful conclusion.
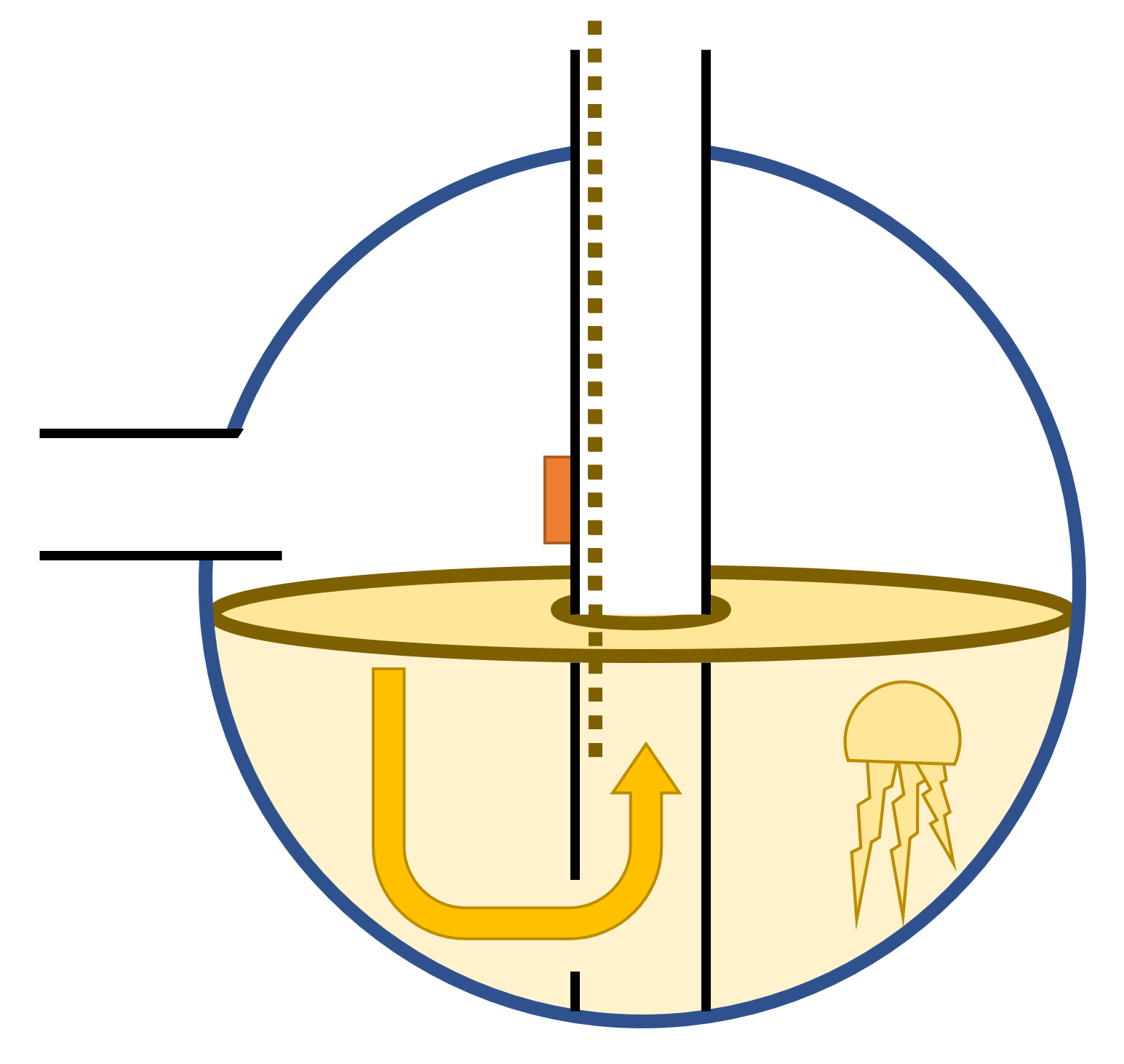Secret Chimney Puzzle
Goblin's Henchman 